学习资料-应付考试版
考纲:
- 排队论模型:学习简单的排队论模型的建模方法,熟悉和掌握排队系统中的平均队长、平均顾客数、系统中顾客退留时间、队列中顾客等待时间等的计算。
- 规划论模型:学习掌握数学规划:线性规划、整数规划、目标规划、动态规划等相关概念和理论,并且要求能用相关的方法建立对应的数学规划模型和求解。
- 插值与拟合建模:掌握曲线拟合、插值的基本方法,学会用插值、拟合作数据处理。
- 回归分析模型:学习掌握线性回归与非线性回归的相关概念和理论,并且要求能用相关的最小二乘方法建立对应的回归分析模型,井能进行相关的概率统计进行检验。
- 差分方程模型:了解差分法的基本思想,学会建立实际问题的离散模型,掌握递推、迭代法等求解过程,理解和掌握蛛网模型、银行货款等问题。
- 常微分方程模型:熟悉微分方程建模的基本步骤,掌握线性微分方程建模基本方法,了解非线性微分方程模型的一些特殊性质:熟悉微分方程的解法。
- 决策论模型:掌握決策论的基本理论及其应用。
- 图和网络模型:掌握最短路、最小生成树、最大流等的原理与求解。
一、排队论模型
。。。
二、规划论模型
见张瑛瑛资料
三、插值与拟合模型
。。。
四、回归分析模型
-
回归:是一种统计分析方法,用于预测一个连续变量与一个或多个其他变量之间的关系。
-
线性回归:是回归分析的一种,假设因变量与自变量之间存在线性关系,即因变量与自变量的关系可以用一条直线来描述。
-
非线性回归:是回归分析的一种,假设因变量与自变量之间不存在线性关系,即因变量与自变量的关系不能用一条直线来描述,需要用更复杂的函数模型来描述。
一元线性回归模型:$ y = \beta_0 + \beta_1 x$
$$\color{red}\begin{cases} 斜率 \beta_1:\frac{\sum_{i=1}^n x_i y_i - n \bar{x} \bar{y}}{\sum_{i=1}^n x_i^2 - n \bar{x}^2} \\ 截距 \beta_0:\bar{y} - \beta_1 \bar{x}\end{cases}$$
检验方法:课本是假设检验判断是否为线性,真题没有考
五、差分方程
差分:$\Delta y_{x} = y_{x+1} - y_{x}$
二阶差分:$\Delta {\Delta y_{x}} = \Delta^2 y_{x} = y_{x+2} - 2y_{x+1} +y_{x}$
一阶线性差分方程的一般形式为:$ y_{x+1} = ay_x + f(x)$
-
齐次方程: 如果 $f(x) = 0$,方程变为齐次方程:$ y_{x+1} = ay_x $
其解为:
$$ \color{red}{y_x = C a^x} $$ -
非齐次方程:
- 如果 $f(x) = b$:
递推得其解为:
$$ \color{red}{f(n) = \begin{cases} bx+c & \text{, } a = 1 \\ \frac{b}{1-a}+C\cdot a^x & \text{, } a \neq 1 \end{cases}}$$
- 如果 $f(x) = (a_0 + a_1x + \cdots + a_nx^n)b^x$
其特解为(记得还要加通解也就是对应齐次方程的解):
$$\color{red}{y_x^* = x^k(A_0 + A_1x + \cdots + A_nx^n) \cdot b^x \\ 其中 A 根据 f(x)多项式系数判断,k = \begin{cases} 0 & \text{, } a \neq b \\ 1 & \text{, } a =b \end{cases}}$$
例题:某城市 2020 年汽车保有量 32 万辆,预计此后每年报废上一年的汽车保有量的 6%,并且每年新增汽车数量相同。为保护城市环境,该城市计划到 2035 年汽车保有量不超过 50 万辆,那么每年新增汽车数量不应超过多少辆?($(0.94)^{15} = 0.395$)
解:设第 n 年的汽车保有量为$a_n$,每年新增汽车数量为 x。
-
由题:$a_n = 0.94a_{n-1} + x$
-
其通解为: $a_n = C(0.94)^n + \frac{x}{1-0.94}$ 其中 C 是常数,需要根据初始条件确定
-
利用初始条件 $a_0 = 32$,我们可以求出 C: $32 = C + \frac{x}{0.06}$ $C = 32 - \frac{x}{0.06}$
-
即: $a_n = (32 - \frac{x}{0.06})(0.94)^n + \frac{x}{0.06}$
-
现在,需要满足 15 年后不超过 50 万辆的条件: $a_{15} ≤ 50$
-
代入 n=15 到刚刚的解: $(32 - \frac{x}{0.06})(0.94)^{15} + \frac{x}{0.06} ≤ 50$
得:$x≤ 3.71$万
六、常微分方程模型
。。。
七、决策论模型
一般会根据乐观准则、悲观准则、折衷主义准则进行决策
过程其实很简单:
- 先看列,乐观准则找每列最大值,悲观准则找每列最小值,折衷主义准则算出$(每列最大值)\cdot \lambda +(每列最小值) \cdot (1-\lambda)$
- 找到后取最大值
例题: 某公司将推出一种新产品,有三种推广方案:让利销售 $(d_1)$,送货上门 $(d_2)$,不采取措施$(d_3)$。未来市场可能有畅销 $s_1$、一般$s_2$、滞销 $s_3$三种状态。假设事先不知道这三种自然状态的出现的概率,但知道各种状态下各方案的盈利,见表。请用以上介绍的 3 种决策方法进行决策(乐观系数 $\alpha = 0.6$)。
| 市场状态 | 畅销 $s_1$ | 一般 $s_2$ | 滞销 $s_3$ |
|---|---|---|---|
| 方案 | 盈利 | 盈利 | 盈利 |
| 让利销售 $(d_1)$ | 60 | 10 | -6 |
| 送货上门 $(d_2)$ | 30 | 25 | 0 |
| 不采取措施 $(d_3)$ | 10 | 10 | 10 |
解:1、乐观法:$ \underset{i}{max}\text{ }\underset{j}{max}{a_{ij}} $
$max {60, 10, -6} = 60 $
$max {30, 25, 0} = 30$
$max {10, 10, 10} = 10 $
$ \underset{i}{max}\text{ }\underset{j}{max}{a_{ij}} =60 $
对应的最优方案为 $(d_1)$。
- 悲观法:$ \underset{i}{max}\text{ }\underset{j}{min}{a_{ij}} $
$min {60, 10, -6} = -6 $
$min {30, 25, 0} = 0 $
$min {10, 10, 10} = 10 $
$ \underset{i}{max}\text{ }\underset{j}{min}{a_{ij}} =10$
对应的最优方案为 $(d_3)$。
- 乐观系数法 $\alpha = 0.6$:
$CV_1 = 0.6 \times 60 + 0.4 \times (-6) = 33.6 $
$CV_2 = 0.6 \times 30 + 0.4 \times 0 = 18 $
$CV_3 = 0.6 \times 10 + 0.4 \times 10 = 10 $
$\max {33.6, 18, 10} = 33.6 $
故最优方案为 $(d_1)$。
八、图和网络模型
最短路径问题
最短路径是把两点之间路径最短的问题,它只着眼于点与点之间的路径问题,并不关注整个图,也就意味着对一个节点运行算法的结果与另一个节点的结果之间没有多少关系。
Dijkstra 算法:
-
步骤
- 初始化:设置起始顶点的距离为 0,其他所有顶点的距离为无限大。起始顶点加入未处理顶点集合。
- 选择未处理顶点集合中距离起始顶点最近的顶点作为当前顶点。
- 更新当前顶点的邻居顶点的距离(如果通过当前顶点到达邻居顶点的路径更短,则更新邻居顶点的距离)。
- 将当前顶点标记为已处理,并从未处理顶点集合中移除。
- 重复步骤 2-4,直到处理完所有顶点或目标顶点的距离不再更新。
最小生成树问题
最小生成树是把连通的图的所有顶点连起来路径之和最小的问题,即生成树总权值之和最小。即在一个连通的图里,如何去除图里的边,使得剩余的边仍能连接所有的节点,且这些边的权重之和最小。
Kruskal 算法:
- 步骤
- 初始化一个空的生成树。
- 依次选择权重最小的边,如果这条边加入生成树后不形成环,则将其加入生成树。
- 重复步骤 2,直到生成树包含图中的所有顶点。
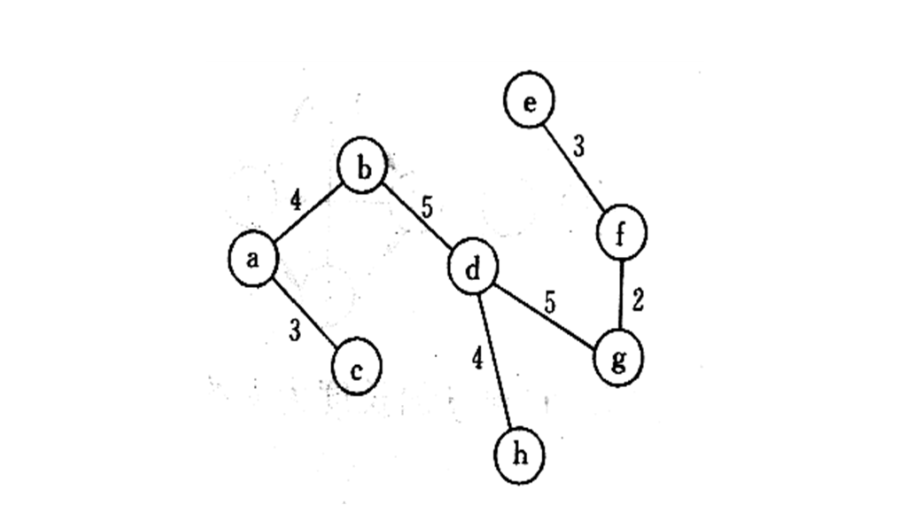
例题:找到 6.33 图的最小生成树!例题2
答案: