SVM 支持向量机

写这篇博客时看到知乎一篇 16 年的文章，作者指出传统 SVM 在对一些稀奇古怪的样本进行分类时有比较好的效果，但是评论区纷纷表示：多来几层神经网络就搞定了。由于我知识储备有限，在此就简单讲讲我的理解。

SVM基本形式求解

给定一个二分类问题的训练样本集：

$D=(x_1,y_1),(x_2,y_2),…,(x_m,y_m),y_i∈−1,+1$¹，

我们的目标是找到一条分界线/超平面²来将两类区分开，如下图：

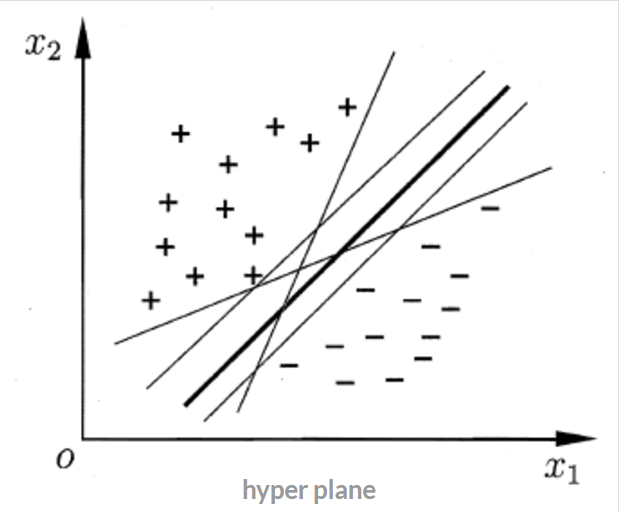
• $w=(w_1,w_2,…,w_d)$ 为法向量，决定了超平面的方向
• $b$ 为位移项，决定了超平面与原点的距离。

如果一个超平面能够将训练样本正确分类，则我们希望这个超平面具有的性质是，对于 $(x_i,y_i)∈D$，有： $$f(x) = \begin{cases} w^T x + b \geq 0, & y_i = +1; \ w^T x + b \leq 0, & y_i = -1. \end{cases}$$

换言之，在进行分类的时候，遇到一个新的数据点 $x$，将 $x$ 代入 $f(x)$ 中：

• 如果 $f(x)$ 小于 $0$ ，则将 $x$ 的类别赋为 $-1$
• 如果 $f(x)$ 大于 $0$ ，则将 $x$ 的类别赋为 $1$

接下来的问题是，如何确定这个超平面呢? SVM 算法的标准是使直线离两边的点间隔最大。

间距计算

点到超平面的距离公式³为：

$$\text{distance} = \frac{|w^T x + b|}{||w||}$$

注意到这个距离并未区分样本类别，于是令支持向量满足：

$y_i(w^T x_i + b) = λ = 1$⁴

此时得到间距：$\gamma =\frac{2}{||w||}$

最优化问题

$$\begin{aligned} \max & \frac{2}{||w||} \ ,\quad\text{s.t.} \quad y_i(w^T x_i + b) \geq 1, \quad i = 1,\ldots,n \end{aligned}$$

等价地，可以转化为：

$\begin{aligned} \min & \frac{1}{2}||w||^2 \ \quad\text{s.t.} \quad y_i(w^T x_i + b) \geq 1, \quad i = 1,\ldots,n \end{aligned}$

这是一个凸二次规划问题，可以使用拉格朗日对偶理论求解⁵。

求得模型

具体过程此处不题，得：$f(x)=w^{T}x+b= \sum_{i=1}^m\alpha_i y_i x_i^{T}x+b$